이전 글에서 합성곱 신경망에 등장하는 개념들을 살펴보았다면, 이번 글에서는 이를 적용해 이미지를 분류하는 것을
진행하고자 한다.
패션 MNIST 데이터 불러오기
데이터를 불러오는 과정이 기존의 연결 신경망하고는 약간 다르다.
완전 연결 신경망에서는 이미지를 일렬로 펼쳐야하기 때문에 reshape() 메서드를 사용하거나 Flatten 클래스를
사용했다. 그렇지만, 합성곱 신경망에서는 2차원 이미지를 그대로 사용한다.
그런데 합성곱 신경망에서는 크기에 깊이라는 차원이 더해진 3차원 배열임을 상기해야한다.
기존의 2차원 배열에 차원을 추가하기 위해 reshape() 메서드를 사용하면 되는데 전체 배열 차원을 그대로 유지하면서
마지막에 차원을 추가해보도록 하자.
from tensorflow import keras
from sklearn.model_selection import train_test_split
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
train_scaled = train_input.reshape(-1, 28, 28, 1) / 255.0
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target,
test_size=0.2, random_state=42)
(48000, 28 28) 인 train_input이 (48000, 28, 28, 1)인 train_scaled가 되었다.
합성곱 신경망 만들기
마찬기지로 Sequential() 클래스를 사용하여 순서대로 구조를 정의한다.
첫 번째 합성곱 층인 Conv2D를 추가해보자.
model = keras.Sequential()
model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu', padding='same', input_shape=(28, 28, 1)))
그 다음 풀링층을 추가해보자.
model.add(keras.layers.MaxPooling2D(2))
첫번째 합성곱 - 풀링 층 다음으로 두번째 합성곱 - 풀링 층을 추가해보자.
model.add(keras.layers.Conv2D(64, kernel_size=3, activation='relu', padding='same'))
model.add(keras.layers.MaxPooling2D(2))마지막으로는 3차원 특성 맵을 일렬로 펼쳐서 출력층에 보내보자.
여기에서는 특성 맵을 일렬로 펼쳐서 바로 출력층에 전달하지 않고 중간에 하나의 밀집 은닉층을 하나 더 두자.
model.add(keras.layers.Faltten())
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dropout(0.4))
model.add(keras.layers.Dense(10, activation='softmax'))
은닉층과 출력층 사이에 드롭아웃을 넣었다. 이 드롭아웃 층이 은닉층의 과대적합을 막아 성능을 개선해준다.
패션 MNIST 데이터셋은 클래스 10개를 분류하는 다중 분류 문제이므로 마지막 층의 활성화 함수는 소프트맥스를
사용한다.
이렇게 구성한 케라스 모델의 구조를 출력해보자.
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_3 (Conv2D) (None, 28, 28, 32) 320
max_pooling2d_2 (MaxPooling (None, 14, 14, 32) 0
2D)
conv2d_4 (Conv2D) (None, 14, 14, 64) 18496
max_pooling2d_3 (MaxPooling (None, 7, 7, 64) 0
2D)
flatten (Flatten) (None, 3136) 0
dense (Dense) (None, 100) 313700
dropout (Dropout) (None, 100) 0
dense_1 (Dense) (None, 10) 1010
=================================================================
Total params: 333,526
Trainable params: 333,526
Non-trainable params: 0
_________________________________________________________________첫번째 합성곱 신경망의 output 크기는 세임 패딩을 이용했고, 커널의 갯수를 32개로 지정했으므로 (28, 28, 32) 크기의
출력이 되고, 풀링의 크기가 2이므로 풀링층을 지나면 (14, 14, 32) 크기가 출력이 된다.
그 뒤의 두 번째 합성곱 신경망은 첫 번째 원리와 비슷하므로 설명하진 않겠다.
그래서 두 번째 풀링까지 거치고 난 뒤 출력의 크기는 (7, 7, 64) 가 된다.
모델의 파라미터 갯수를 계산해보면, 첫 번째 합성곱 층은 32개의 필터를 가지고 있고 크기가 (3, 3, 1)이 된다.
그리고 각 필터마다 절편을 가지고 있으므로 3 * 3 * 1 * 32 + 32 = 320개의 파라미터가 있다
두 번째 합성곱 층은 64개의 필터와 (3,3,32) 크기이므로 3 * 3 * 32 * 64 + 64 = 18496개의 파라미터가 있다.
summary() 메서드 외에 층의 구조를 그림으로 표현해주는 plot_model() 함수가 keras.utils에서 제공되고 있다.
keras.utills.plot_model(model)
여기에 입력과 출력의 크기를 표시해주는 show_shape 매개변수가 있다.
keras.utils.plot_model(model, show_shapes=True)
이 과정을 그림으로 살펴보면 다음과 같다.
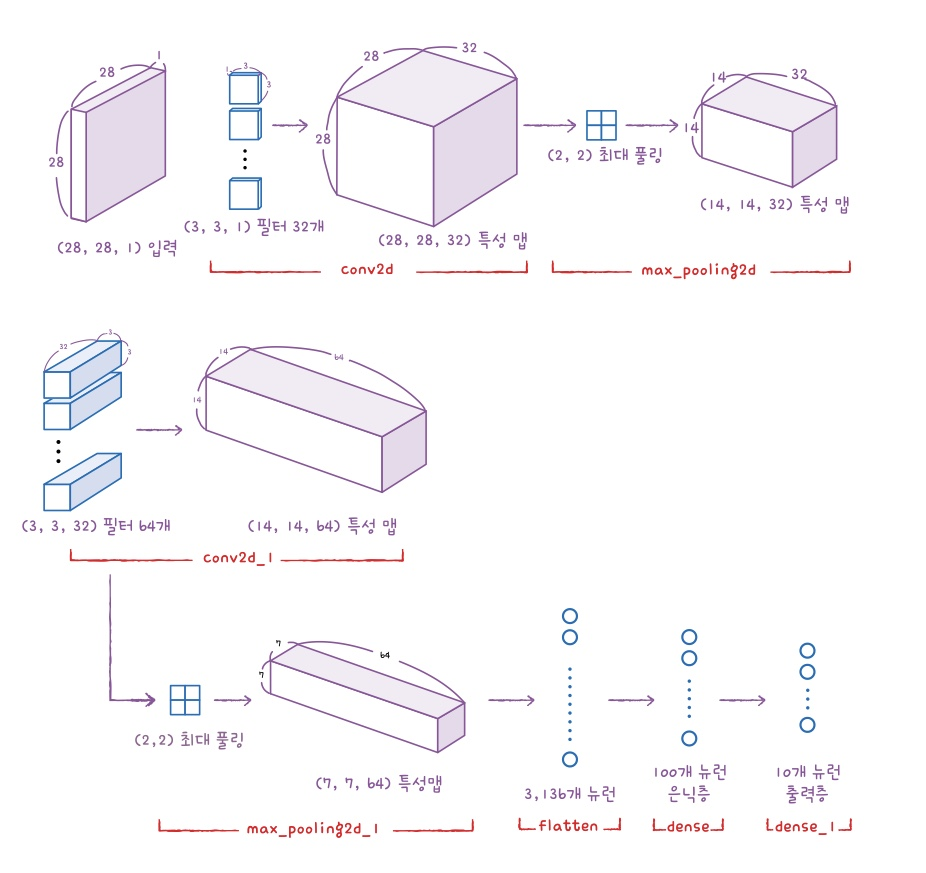
모델 컴파일과 훈련
합성곱 모델의 컴파일과 훈련하는 방법은 완전 연결 신경망 모델의 컴파일과 훈련 방법과 같다.
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics='accuracy')
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-cnn-model.h5', save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2, restore_best_weights=True)
history = model.fit(train_scaled, train_target, epochs=20,
validation_data = (val_scaled, val_target),
callbacks=[checkpoint_cb, early_stopping_cb])
Epoch 1/20
1500/1500 [==============================] - 19s 4ms/step - loss: 0.5207 - accuracy: 0.8154 - val_loss: 0.3248 - val_accuracy: 0.8802
Epoch 2/20
1500/1500 [==============================] - 6s 4ms/step - loss: 0.3478 - accuracy: 0.8754 - val_loss: 0.2796 - val_accuracy: 0.8950
Epoch 3/20
1500/1500 [==============================] - 5s 4ms/step - loss: 0.2960 - accuracy: 0.8937 - val_loss: 0.2530 - val_accuracy: 0.9062
Epoch 4/20
1500/1500 [==============================] - 6s 4ms/step - loss: 0.2625 - accuracy: 0.9051 - val_loss: 0.2519 - val_accuracy: 0.9076
Epoch 5/20
1500/1500 [==============================] - 6s 4ms/step - loss: 0.2399 - accuracy: 0.9124 - val_loss: 0.2266 - val_accuracy: 0.9137
Epoch 6/20
1500/1500 [==============================] - 6s 4ms/step - loss: 0.2193 - accuracy: 0.9207 - val_loss: 0.2330 - val_accuracy: 0.9156
Epoch 7/20
1500/1500 [==============================] - 5s 4ms/step - loss: 0.2022 - accuracy: 0.9260 - val_loss: 0.2290 - val_accuracy: 0.9148위는 adam 옵티마이저를 사용하고 modelcheckpoint 콜백과 earlystopping 콜백을 함께 사용한 것이다.
손실 그래프를 그려서 조기 종료가 잘 이루어졌는지 확인해보자.
import matplotlib.pyplot as plt
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
검증 세트에 대한 손실이 점차 감소하다가 정체되고, 훈련 세트에 대한 손실은 점점 낮아지고 있다.
위에 EarlyStopping 클래스에서 restore_best_weights 매개변수를 True로 지정했으므로 현재 model 객체가
최적의 모델 파라미터로 복원되어 있다.
즉 ModelCheckpoint 콜백이 저장한 best-cnn-model.h5 파일을 다시 읽을 필요가 없다.
이번에는 세트에 대한 성능을 평가해보자.
model.evaluate(val_scaled, val_target)
375/375 [==============================] - 1s 2ms/step - loss: 0.2266 - accuracy: 0.9137
[0.22659213840961456, 0.9137499928474426]
위에서 5 번째 에포크의 출력과 같은 것을 알 수 있다.
그러면 이 모델을 이용해서 predict() 메서드를 이용, 새로운 데이터에 대한 예측을 만들어 보자.
plt.imshow(val_scaled[0].reshape(28, 28), cmap='gray_r')
plt.show()
첫 번째 샘플 이미지는 핸드백이다.
먼저 샘플 이미지를 확인했고, predict() 메서드를 이용해 10개 클래스에 대한 예측 확률을 출력해보자.
preds = model.predict(val_scaled[0:1])
print(preds)
[[3.5941309e-12 1.7034785e-16 1.0179603e-12 4.2053383e-13 7.8666761e-11
1.6891747e-12 4.1003892e-10 1.4163858e-11 1.0000000e+00 6.3542301e-12]]9번째를 제외하고 나머지는 0에 수렴한다. 9번째 값은 1이 된다.
이를 막대 그래프로 그리면 확실히 볼 수 있다.
plt.bar(range(1, 11), preds[0])
plt.xlabel('class')
plt.ylabel('prob.')
plt.show()
파이썬에서 레이블을 다루기 위해 리스트로 저장하고, preds 배열에서 가장 큰 인덱스를 찾아 classes 리스트의 인덱스로
사용해보자.
classes = ['티셔츠', '바지', '스웨터', '드레스', '코트', '샌달', '셔츠', '스니커즈', '가방', '앵클 부츠']
import numpy as np
print(classes[np.argmax(preds)])
가방샘플을 가방으로 예측한 것을 볼 수 있다.
이번에는 테스트 셋을 모델에 넣어 평가 해본다.
test_scaled = test_input.reshape(-1, 28, 28, 1) / 255.0
model.evaluate(test_scaled, test_target)
313/313 [==============================] - 1s 3ms/step - loss: 0.2465 - accuracy: 0.9102
[0.2464602291584015, 0.9101999998092651]
'Study > 혼자 공부하는 머신러닝' 카테고리의 다른 글
| 혼자 공부하는 머신러닝 + 딥러닝 - 합성곱 신경망의 시각화 (0) | 2022.04.27 |
|---|---|
| 혼자 공부하는 머신러닝 + 딥러닝 - 합성곱 신경망의 구성요소 (1) | 2022.04.26 |
| 혼자 공부하는 머신러닝 + 딥러닝 - 신경망 모델 훈련 (0) | 2022.04.21 |
| 혼자 공부하는 머신러닝 + 딥러닝 - 심층 신경망 (0) | 2022.04.21 |
| 혼자 공부하는 머신러닝 - 인공 신경망 (0) | 2022.04.07 |



